Parsing floating point numbers
The first task is extending the LispVal type to grok floats.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
type LispInt = Integer
type LispFloat = Float
-- numeric data types
data LispNum = Integer LispInt
| Float LispFloat
-- data types
data LispVal = Atom String
| List [LispVal]
| DottedList [LispVal] LispVal
| Number LispNum
| Char Char
| String String
| ...
The reason for using the new LispNum type and not just throwing a new Float Float constructor in there is so that functions can accept and operate on parameters of any supported numeric type. First the floating point numbers need to be parsed. For now I only parse floating point numbers in decimal because the effort to parse other bases is too great for the benefits gained (none, for me).
ElSchemo now parses negative numbers so I'll start with 2 helper functions that are used when parsing both integers and floats:
1
2
3
4
5
6
7
parseSign :: Parser Char
parseSign = do try (char '-')
<|> do optional (char '+')
return '+'
applySign :: Char -> LispNum -> LispNum
applySign sign n = if sign == '-' then negate n else n
parseSignis straightforward as it follows the convention that a literal number is positive unless explicitly marked as negative with a leading minus sign. A leading plus sign is allowed but not required.
applySigntakes a sign character and a LispNum and negates it if necessary, returning a LispNum.
Armed with these 2 functions we can now parse floating point numbers in decimal. Conforming to R5RS an optional #d prefix is allowed.
1
2
3
4
5
6
7
8
parseFloat :: Parser LispVal
parseFloat = do optional (string "#d")
sign <- parseSign
whole <- many1 digit
char '.'
fract <- many1 digit
return . Number $ applySign sign (makeFloat whole fract)
where makeFloat whole fract = Float . fst . head . readFloat $ whole ++ "." ++ fract
The first 6 lines should be clear. Line 7 simply applies the parsed sign to the parsed number and returns it, delegating most of the work to makeFloat. makeFloat in turn delegates the work to the readFloat library function, extracts the result and constructs a LispNum for it.
The last step for parsing is to modify parseExpr to try and parse floats.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
-- Integers, floats, characters and atoms can all start with a # so wrap those with try.
-- (Left factor the grammar in the future)
parseExpr :: Parser LispVal
parseExpr = (try parseFloat)
<|> (try parseInteger)
<|> (try parseChar)
<|> parseAtom
<|> parseString
<|> parseQuoted
<|> do char '('
x <- (try parseList) <|> parseDottedList
char ')'
return x
<|> parseComment
Displaying the floats
That's it for parsing, now let's provide a way to display these suckers. LispVal is an instance of show, where show = showVal so showVal is our first stop. Remembering that LispVal now has a single Number constructor we modify it accordingly:
1
2
3
4
5
6
7
showVal (Number n) = showNum n
showNum :: LispNum -> String
showNum (Integer contents) = show contents
showNum (Float contents) = show contents
instance Show LispNum where show = showNum
One last, and certainly not least, step is to modify eval so that numbers evaluate to themselves.
eval env val@(Number _) = return val
There's a little more housekeeping to be done such as fixing integer?, number?, implementing float? but I will leave those as an exercise to the reader, or just wait until I share the full code. As it stands now floating point numbers can be parsed and displayed. If you fire up the interpreter and type 2.5 or -10.88 they will be understood. Now try adding them:
(+ 2.5 1.1) Invalid type: expected integer, found 2.5
Oops, we don't know how to operate on floats yet!
Operating on floats
Parsing was the easy part. Operating on the new floats is not necessarily difficult, but it was more work than I realized it would be. I don't claim that this is the best or the only way to operate on any LispNum, it's just the way I did it and it seems to work. There's a bunch of boilerplate necessary to make LispNum an instance of the required classes, Eq, Num, Real, and Ord. I don't think I have done this properly but for now it works. What is clearly necessary is the code that operates on different types of numbers. I think I've specified sane semantics for coercion. This will be very handy shortly.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
lispNumEq :: LispNum -> LispNum -> Bool
lispNumEq (Integer arg1) (Integer arg2) = arg1 == arg2
lispNumEq (Integer arg1) (Float arg2) = (fromInteger arg1) == arg2
lispNumEq (Float arg1) (Float arg2) = arg1 == arg2
lispNumEq (Float arg1) (Integer arg2) = arg1 == (fromInteger arg2)
instance Eq LispNum where (==) = lispNumEq
lispNumPlus :: LispNum -> LispNum -> LispNum
lispNumPlus (Integer x) (Integer y) = Integer $ x + y
lispNumPlus (Integer x) (Float y) = Float $ (fromInteger x) + y
lispNumPlus (Float x) (Float y) = Float $ x + y
lispNumPlus (Float x) (Integer y) = Float $ x + (fromInteger y)
lispNumMinus :: LispNum -> LispNum -> LispNum
lispNumMinus (Integer x) (Integer y) = Integer $ x - y
lispNumMinus (Integer x) (Float y) = Float $ (fromInteger x) - y
lispNumMinus (Float x) (Float y) = Float $ x - y
lispNumMinus (Float x) (Integer y) = Float $ x - (fromInteger y)
lispNumMult :: LispNum -> LispNum -> LispNum
lispNumMult (Integer x) (Integer y) = Integer $ x * y
lispNumMult (Integer x) (Float y) = Float $ (fromInteger x) * y
lispNumMult (Float x) (Float y) = Float $ x * y
lispNumMult (Float x) (Integer y) = Float $ x * (fromInteger y)
lispNumDiv :: LispNum -> LispNum -> LispNum
lispNumDiv (Integer x) (Integer y) = Integer $ x `div` y
lispNumDiv (Integer x) (Float y) = Float $ (fromInteger x) / y
lispNumDiv (Float x) (Float y) = Float $ x / y
lispNumDiv (Float x) (Integer y) = Float $ x / (fromInteger y)
lispNumAbs :: LispNum -> LispNum
lispNumAbs (Integer x) = Integer (abs x)
lispNumAbs (Float x) = Float (abs x)
lispNumSignum :: LispNum -> LispNum
lispNumSignum (Integer x) = Integer (signum x)
lispNumSignum (Float x) = Float (signum x)
instance Num LispNum where
(+) = lispNumPlus
(-) = lispNumMinus
(*) = lispNumMult
abs = lispNumAbs
signum = lispNumSignum
fromInteger x = Integer x
lispNumToRational :: LispNum -> Rational
lispNumToRational (Integer x) = toRational x
lispNumToRational (Float x) = toRational x
instance Real LispNum where
toRational = lispNumToRational
lispIntQuotRem :: LispInt -> LispInt -> (LispInt, LispInt)
lispIntQuotRem n d = quotRem n d
lispIntToInteger :: LispInt -> Integer
lispIntToInteger x = x
lispNumLessThanEq :: LispNum -> LispNum -> Bool
lispNumLessThanEq (Integer x) (Integer y) = x <= y
lispNumLessThanEq (Integer x) (Float y) = (fromInteger x) <= y
lispNumLessThanEq (Float x) (Integer y) = x <= (fromInteger y)
lispNumLessThanEq (Float x) (Float y) = x <= y
instance Ord LispNum where (<=) = lispNumLessThanEq
Phew, ok with that out of the way now we can actually extend our operators to work with any type of LispNum. Our Scheme operators are defined using the functions numericBinop and numBoolBinop. First we'll slightly modify our definition of primitives:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
primitives :: [(String, [LispVal] -> ThrowsError LispVal)]
primitives = [("+", numericBinop (+)),
("-", subtractOp),
("*", numericBinop (*)),
("/", floatBinop (/)),
("mod", integralBinop mod),
("quotient", integralBinop quot),
("remainder", integralBinop rem),
("=", numBoolBinop (==)),
("<", numBoolBinop (<)),
(">", numBoolBinop (>)),
("/=", numBoolBinop (/=)),
(">=", numBoolBinop (>=)),
("<=", numBoolBinop (<=)),
...]
Note that mod, quotient, and remainder are only defined for integers and as such use integralBinop, while division (/) is only defined for floating point numbers using floatBinop. subtractOp is different to support unary usage, e.g. (- 4) => -4, but it uses numericBinop internally when more than 1 argument is given. On to the implementation! First extend unpackNum to work with any LispNum, and provide separate unpackInt and unpackFloat functions to handle both kinds of LispNum.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
unpackNum :: LispVal -> ThrowsError LispNum
unpackNum (Number (Integer n)) = return $ Integer n
unpackNum (Number (Float n)) = return $ Float n
unpackNum notNum = throwError $ TypeMismatch "number" notNum
unpackInt :: LispVal -> ThrowsError Integer
unpackInt (Number (Integer n)) = return n
unpackInt (List [n]) = unpackInt n
unpackInt notInt = throwError $ TypeMismatch "integer" notInt
unpackFloat :: LispVal -> ThrowsError Float
unpackFloat (Number (Float f)) = return f
unpackFloat (Number (Integer f)) = return $ fromInteger f
unpackFloat (List [f]) = unpackFloat f
unpackFloat notFloat = throwError $ TypeMismatch "float" notFloat
The initial work of separating integers and floats into the LispNum abstraction, and the code I said would be handy shortly, are going to be really handy here. There's relatively no change in numericBinop except for the type signature. integralBinop and floatBinop are just specific versions of the same function. I'm sure there's a nice Haskelly way of doing this with less repetition, and I welcome such corrections.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
numericBinop :: (LispNum -> LispNum -> LispNum) -> [LispVal] -> ThrowsError LispVal
numericBinop op singleVal@[_] = throwError $ NumArgs 2 singleVal
numericBinop op params = mapM unpackNum params >>= return . Number . foldl1 op
integralBinop :: (LispInt -> LispInt -> LispInt) -> [LispVal] -> ThrowsError LispVal
integralBinop op singleVal@[_] = throwError $ NumArgs 2 singleVal
integralBinop op params = mapM unpackInt params >>= return . Number . Integer . foldl1 op
floatBinop :: (LispFloat -> LispFloat -> LispFloat) -> [LispVal] -> ThrowsError LispVal
floatBinop op singleVal@[_] = throwError $ NumArgs 2 singleVal
floatBinop op params = mapM unpackFloat params >>= return . Number . Float . foldl1 op
subtractOp :: [LispVal] -> ThrowsError LispVal
subtractOp num@[_] = unpackNum (head num) >>= return . Number . negate
subtractOp params = numericBinop (-) params
numBoolBinop :: (LispNum -> LispNum -> Bool) -> [LispVal] -> ThrowsError LispVal
numBoolBinop op params = boolBinop unpackNum op params
That was a bit of work but now ElSchemo supports floating point numbers, and if you're following along then your Scheme might too if I haven't missed any important details!
Next time I'll go over some of the special forms I have added, including short-circuiting and and or forms and the full repetoire of let, let*, and letrec. Stay tuned!
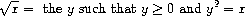This describes a perfectly legitimate mathematical function. We could use it to recognize whether one number is the square root of another, or to derive facts about square roots in general. On the other hand, the definition does not describe a procedure. Indeed, it tells us almost nothing about how to actually find the square root of a given number. It will not help matters to rephrase this definition in pseudo-Lisp: